When I was a solitary, bespectacled and distinctly oikotropic child growing up in Dundee, I was fascinated by the little roundabout, like the one pictured above, in the play area of my local park. While my compatriots were trying their best to kill or maim themselves by using the swings, the slide and the witch’s hat for purposes their designers had neither intended nor dreamed of, I would spin up the roundabout, climb aboard, and try to kick the central pillar.

What was fascinating was that I kept missing. Despite my well-known inability to kick a football, even I shouldn’t have missed a thick metal pillar from a distance of less than a foot. But some mysterious force kept taking hold of my foot as soon as I moved it,  and shoving it sideways. The deflection was there on the backswing, too—if my foot was displaced to my right when I kicked, it was displaced to my left when I swung it back. And I could reverse the direction of deflection by reversing the rotation of the roundabout. Anticlockwise displaced my foot right; clockwise displaced it left. If I turned sideways and swung my foot back and forth tangential to the rotation, the displacement was still there, and in exactly the same direction relative to my body. With a bit of thought, it was evident that no matter what direction I swung my foot while standing on an anticlockwise-spinning roundabout, the foot was always shoved to the right of its direction of travel. Clockwise rotation brought left displacement.

It was almost eerie, and it lodged so firmly in my mind that, a decade later, when my physics teacher described Coriolis force to our little class, I said “Ooooooh! I see!” very loudly and appreciatively. (This was as well received as you might imagine. Which is to say, not.)

Coriolis force (named for Gaspard-Gustave de Coriolis) is a companion to centrifugal force, which I’ve written about before. They’re both often called pseudo-forces, because they only show up if we adopt a rotating reference frame—I described this in detail in my previous post, Saying “Centrifugal” Doesn’t Mean You’re A Bad Person. They’re also called inertial forces, because they arise from the tendency of objects in motion to  follow straight-line paths. Just staying stationary relative to a rotating reference frame (as I did when I stood on my whirling roundabout) means that you experience centrifugal force—what is stationary to you and the roundabout is a continuously curving path in the non-rotating world, and so you experience a constant inertial outward tug as your body tries to fly off in a straight line.

In contrast to centrifugal force, which is there all the time, Coriolis only shows up when you move around. A route that is a straight line across a turning roundabout is a curved path in the non-rotating world, and so whenever you move around in a rotating reference frame you feel a new, nagging inertial tug, trying to drag you away from the “straight” line you want to follow, and to make you move instead in a straight line relative to the outside world (which is a curved path relative to the roundabout).

Where does Coriolis come from? Go back to my attempts to kick the central pillar of the roundabout as it rotates anticlockwise. As my foot swings through a short fore-and-aft kick, aimed directly at the pillar, the roundabout rotates—turning my body anticlockwise and shifting me bodily to the right. My foot, moving with its original velocity, misses the pillar to the right, and is now swinging diagonally relative to my body. But as far as I’m concerned, stationary relative to my rotating reference frame, some mysterious force has seized my foot and curved its trajectory to the right.

If I turn and kick outwards, the same shift and rotation occurs, and my foot swings rightwards relative to my body again.

Face in the direction of spin, or against the direction of spin—it’s always the same rotation and shift. In fact, it doesn’t matter where I stand on the roundabout, or which direction I kick in—the same rotation and shift is always there, so the kick always deviates in the same direction, and by the same amount.

As it turns out, the magnitude of the Coriolis acceleration depends on only two things—it increases the faster your reference frame rotates, and it increases as you move faster relative to the rotating frame. And the direction depends on only one thing—it is always at right angles to the direction of movement, and it pushes rightwards in anticlockwise-rotating systems, and leftwards in clockwise-rotating systems. (And, of course, if you lay underneath my anticlockwise roundabout and looked up at it from below, it would be rotating clockwise to you, and all the deviations in my diagrams would be leftwards.)

All of this applies in the plane of rotation. If you move parallel to the axis of rotation (in and out of the computer screen in my diagrams) then you’re not shifting around in the plane of rotation, and there’s no Coriolis effect. If I’d had the presence of mind to try some squats while on my roundabout, my head wouldn’t have been deflected from its vertical path as I bobbed up and down. (I’m actually slightly ashamed of my eight-year-old self for not coming up with that pretty obvious experiment at the time.)

As I mentioned in my previous post about inertial forces, Coriolis is a bit of a problem for long-duration space exploration. It would be nice to create spinning habitats that simulated gravity using centrifugal force, like the ones featured in the film 2001: A Space Odyssey:

But if they were as small as the one Arthur C. Clarke and Stanley Kubrick but in the spaceship Discovery, above, they’d need to spin fairly fast to produce a useful level of simulated gravity, which would produce significant Coriolis effects. Any movements in the plane of rotation (“up” and “down” in the centrifugal gravity, or around the curve of the habitat in either direction) would be deflected, making it difficult to perform physical tasks. Perhaps more importantly, the liquid in the semi-circular canals of the inner ear would suffer Coriolis deflection whenever the astronauts moved their heads, causing motion sickness and dizziness. Early studies in the 1960s suggested that any habitat rotation rate over 6 rpm would induce disabling motion sickness, but that limit seems to have been too conservative—with slow adaptation, rates of 10-20 rpm may be acceptable*. This means that the compact Discovery centrifuge in Kubrick’s film is more plausible now than when it was first released—surely a first for physical special effects in science fiction films.

For another demonstration of Coriolis deflection, here’s the sort of thing that would happen if you dropped something in a rotating space station. Viewed from outside the station, the object would start to travel in a straight line as soon as you released it, and would continue to move in that direction until it hit the deck. Meanwhile, you would rotate alongside it as the station rotated. The diagram shows your position and that of the dropped object in four successive snapshots.

And here’s what it would look like to you, standing inside the station:

[If you’re interested in finding out more about the trajectories of objects launched in various directions inside a rotating space habitat, I’ve now written an entire post on that topic.]

Science fiction writers love this stuff, though they sometimes (well, often) get the detail wrong. In his novel 2312, Kim Stanley Robinson had Coriolis acting on movements parallel to the rotation axis of his habitat; and in the novel series The Expanse, the two authors who write as James S.A. Corey depict the Coriolis force varying from place to place within their rotating habitat.

That said, there was a valiant attempt to depict Coriolis in action in the television series of The Expanse. Here it is, deflecting a drink being poured:

The trajectory isn’t correct, but it’s still a thing of beauty.

But does Coriolis have any effect outside of the playground and science fiction? Very much so. Planet Earth behaves like a gigantic and slowly revolving roundabout—turning anticlockwise as you look down on the north pole, and clockwise as seen from over the south pole. So Coriolis forces deflect to the right in the northern hemisphere, and to the left in the southern hemisphere. But they don’t do very much at all near the equator—moving north or south at the equator takes you mainly parallel to the Earth’s axis, so doesn’t produce much Coriolis deflection. Moving west or east produces a larger Coriolis force, since you’re moving in the plane of rotation, but it is directed vertically, making you either a little heavier or a little lighter, rather than deflecting your direction of motion.

But away from the equator it’s Coriolis that generates the circulation of ocean currents, which tend to turn rightwards in clockwise gyres in the north, and leftwards in anticlockwise gyres in the south.

The major wind systems are deflected by Coriolis too, drifting westwards as they approach the equator, and eastwards as they recede from it.

And tropical storms and other low pressure regions  spin counterclockwise in the north and clockwise in the south, because of Coriolis. As air flows towards the centre of the low pressure area, it is deflected sideways and ends up flowing around the central low pressure, constantly being pulled inwards by the pressure gradient, but outwards by Coriolis.

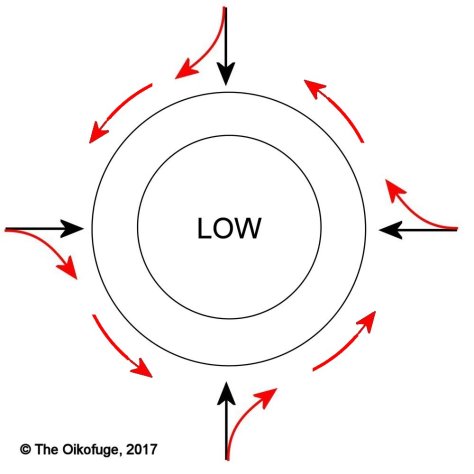
All these are big things, you’ll notice. The Earth rotates slowly, the Coriolis forces are correspondingly weak, and they therefore need to operate for some time before they build up a noticeable deflection. This is all summed up by a ratio called the Rossby number (named for Carl-Gustaf Rossby):

Ro = U/Lf

U is the characteristic velocity and L is the characteristic length of the phenomenon you’re interested in. The f is something called the Coriolis parameter, which for situations that apply to the Earth’s rotation equals 2Ω sinφ, where Ω is the rotation rate of the Earth, and φ is the latitude (to allow for the fact that Coriolis is less effective at the equator, for reasons given above). At mid-latitudes f is equal to about 0.0001.

A small Rossby number (around one or lower) tells us that the length scale of our phenomenon is large enough in comparison to the velocity that Coriolis will have enough time to build up a significant deflection^†. A high Rossby number, on the other hand, tells us that Coriolis simply doesn’t have time to work, and that other forces in the environment will likely overwhelm its effect. The big oceanic and atmospheric phenomena I mentioned above operate at velocities on the order of ten metres per second, over distances of hundreds of kilometres, which places them at a range of Rossby numbers between 0.1 and 1, where Coriolis is significant.

Which brings me to bathtubs and toilet bowls, and the assertion that these objects drain in opposite directions in opposite hemispheres. Here, we have a phenomenon on the scale of a metre, with velocities of around a metre per second. That’s a Rossby number of ten thousand. The water flow is simply too fast for the scale, and Coriolis has no chance to produce a significant deflection—instead, the rotation of the drain vortex will depend on local factors like the shape of the bath, the swirl produced when the plug is pulled, and the direction in which the flush pipe of the toilet points.

But if you visit the equator, you’ll find people who appear to be demonstrating the Coriolis effect, on water draining from bowls placed just a few metres either side of the line.  Now, remember, the equator is the worst place on Earth to try to demonstrate this, because Coriolis forces operate so weakly there—ten metres north or south of the equator the Coriolis parameter (described above) is about 2.5×10^-10, giving a Rossby number for a draining bowl of around four billion. That’s four billion. I think we can all agree that’s significantly greater than one.

But here’s a demonstration, from Michael Palin’s television series, Pole to Pole:

And another:

Remarkable, eh? Especially since the water drains the wrong way for the phenomenon they’re purporting to demonstrate. If Coriolis were at work, the drainage should behave like the flow into a low pressure system—anticlockwise in the north, clockwise in the south. Perhaps the demonstrators were confused into reproducing the rotation of the ocean gyres—but those are driven by tides and winds, not by a great big plughole in the middle of the Pacific.

So what you’re actually seeing demonstrated are two ways to generate whatever drainage swirl you want. In the first example, take a square bowl and make sure you turn to face your audience with the same rotation you want the water to follow—your turn will set the water swirling in the desired direction. In the second, change the shape of the bowl to favour a particular direction of drainage—for instance, by painting a big thick spiral of paint on the bottom of it.

Finally, here’s another, who gets an award for at least making the water swirl in the right direction, but a demerit for being so transparent about how she’s manufacturing the flow with her big bucket of water and her off-centre pouring style:

---

* Clément GR, Bukley AP and Paloski WH (2015) Artificial gravity as a countermeasure for mitigating physiological deconditioning during long-duration space missions. Front. Syst. Neurosci. 9:92.

^† If you’re thinking back to the fact that high velocity incurs high Coriolis force, you’re maybe wondering why the Rossby number favours low velocities. What’s happening is that high velocities get you to your destination faster, giving less time for the Coriolis forces to work. The distance travelled at a given velocity is proportional to the elapsed time, but the distance travelled at constant acceleration is proportional to time squared. Doubling the velocity gets you to your destination in half the time, and so the doubled Coriolis acceleration causes only half the deflection. (If I’d fired a gun at the central pillar of the roundabout, instead of kicking it, I’d have hit my target easily. There might have been other problems, though.)