 The year 2020, newly begun as this post is published, is a leap year. I’ve written before about leap years, and how the occasional leap day added to the end of February keeps our calendar year synchronized with the seasons. For more on that topic, see my posts about February 30th and the Equinox.
The year 2020, newly begun as this post is published, is a leap year. I’ve written before about leap years, and how the occasional leap day added to the end of February keeps our calendar year synchronized with the seasons. For more on that topic, see my posts about February 30th and the Equinox.
But this year we are also fairly likely to observe a leap second. (I’ll come back later to the reason for that “fairly likely”.) A leap second is an additional second which will be added to either June 30th or December 31st, and it serves to keep our clocks synchronized with the rotation of the Earth.
The fundamental problem is that the Earth’s rotation is getting slower, primarily because the tidal bulges raised in the Earth’s oceans by the moon and sun generate friction in the ocean beds as the Earth rotates. Over the last couple of millennia the rate of slowing has averaged about 1.7 milliseconds per day, per century. Which sounds trivial, but it adds up to more than three hours over the last two thousand years. We can detect this problem if we look back at early records of astronomical events, particularly solar eclipses, which are visible from only a very limited region of the Earth’s surface. We know, for instance, that a solar eclipse was observed in Babylon early in the morning of 15 April, 136BC. But if we calculate back to the relative positions of the sun, Earth and moon on that date, and assume the Earth has rotated at a constant rate during the intervening centuries, we find the eclipse shadow sweeping through the Atlas Mountains of Morocco, 48.8º of longitude west of Babylon. The difference in longitude represents a three-hour lag in rotation—the naive calculation, ignoring the tidal slowing of the Earth’s rotation, has allowed Babylon to rotate out from under the eclipse track. That mismatch is one of the ways we know about the long-term slowing of the Earth’s rotation.

Source of base map
Here and now, we have three important ways by which we measure the passage of time. The first, and most important in everyday life, is by the rotation of the Earth. We define local noon as being the time at which the sun reaches its highest point in the sky, and we define a solar day as being the time between successive noons. Well, sort of. Because the Earth’s orbit is elliptical, and the Earth’s axis is tilted relative to its orbit, the elapsed time between successive noons varies during the course of the year. So we average those noon passages over a long time period in order to come up with a definition for the day—specifically, it’s a mean solar day.
This mean solar day is conventionally divided into the familiar hours, minutes and seconds, giving 24×60×60=86400 seconds per day. But you can see that there’s a problem with that, because seconds are of a fixed duration, established and defined as part of the Système International (SI) units in 1960. Whereas we now know that the length of the mean solar day is increasing as the Earth’s rotation slows.
Scientists were aware of this problem when the SI units were being defined, and decided they needed to use some other source, with a more fixed and regular motion, in order to define a constant second. Initially, they resorted to our second important means of time-keeping—the movement of the Earth around the sun. The length of the year is rather closer to being constant than the rotation period of the Earth. So the duration of the second was defined as being 1⁄31,556,925.9747 of a tropical year. (The tropical year is a measure of the passage of the seasons—it’s the year that our calendar strives to approximate with all those leap days.)
So that was fine, then. But not quite, because the tropical year is itself a little variable. So what was adopted as the standard was derived from a very specific (and sort of fictitious) tropical year, based on formulae given in Simon Newcomb’s astronomical opus, The Elements Of The Four Inner Planets And The Fundamental Constants Of Astronomy, published in 1895 and based on astronomical observations made between 1750 and 1892. Specifically, the tropical year on which the SI second was based was something produced by Newcomb’s formulae if you plugged in a precise time and date near the start of 1900. So there was no actual year that corresponded to the value used in the definition. And of course Newcomb, and the observers who provided his data, had never used a constant definition of the second. Their definition was based on a second that was exactly 1/86400 of a mean solar day—so seconds, as defined in 1750, were a tiny bit shorter than seconds as defined in 1892. When Newcomb tabulated all these observational data and produced his summary formulae, he effectively averaged out the very slight drift in the value of the second over the observation period. Newcomb’s second, which became the SI second, was only ever exactly 1/86400 of a mean solar day somewhere around the year 1820. So even at the moment of its adoption in 1960, the SI second was slightly adrift from the duration of a mean solar day.
The astronomical definition of the SI second was always a bit unwieldy for general use. Fortunately, there was a third method of measuring time, which had been growing steadily more precise around the time the SI units were introduced—the atomic clock. So in 1967 the definition of the second was transferred to something you could actually measure in the laboratory—the behaviour of a particular kind of clock based on the element caesium. Thenceforth, the SI second was defined as:
… the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.
So now we have a precise and portable definition of the second, which carries over its duration from a previous astronomical definition, based on nineteenth-century observations. This is the basis for a standard called International Atomic Time (abbreviated TAI, for Temps Atomique International), which is based on pooled readings from multiple atomic clocks around the world.
But the Earth’s rotation is steadily lagging behind TAI. So to keep our everyday clocks in synchrony with the slowly lengthening mean solar day, we use a different time scale called Coordinated Universal Time (confusingly abbreviated UTC), which is the basis for Greenwich Mean Time and all the various time zones around the world.
UTC uses the same SI seconds as TAI, but every now and then needs to pause for a moment to allow the Earth’s rotation to “catch up”. Which is where the leap seconds come in—when required, at the end of a month, we add an extra second just before midnight, Greenwich Mean Time. A clock that displays such leap seconds reads 23:59:60 (as at the head of this post) before cycling through to 00:00:00. This leap second is added everywhere, simultaneously, so it occurs in the afternoon or evening in the Americas, but in the morning in Asia and Australia.
At present, the Earth’s rotation is slowing at about 1.4 milliseconds per day, per century (a little slower than the millennial trend I mentioned earlier). Since two centuries have elapsed since the second was exactly 1/86400 of the mean solar day, the day should now be 86400.0028 seconds long, which corresponds to almost exactly one extra second per year.
So why don’t we just schedule an extra second for every December 31st and have done with it? Because the Earth’s rotation rate varies irregularly, from day to day and year to year, around the long term mean rate of slowing. This happens because stuff (air, water, rock) is always moving around, sometimes shifting closer to the Earth’s axis of rotation, and sometimes farther away. If mass moves closer to the axis, the Earth speeds up a little; if mass moves away from the axis, the Earth slows down—this is caused by the same conservation of angular momentum that allows figure skaters and acrobatic divers to modify their rate of rotation by drawing in or spreading their arms. So earthquakes, glaciers melting and seasonal shifts in the air mass all contribute to the variability of the Earth’s rotation rate.
In the early days of the leap second (which was introduced in 1972) we did indeed have a leap second every year. But the Earth’s rotation rate has actually bucked the trend and speeded up a little of late, so leap seconds have become more sporadic—we had no leap seconds at all between 1999 and 2004, and the most recent was in 2016. The aim of the leap second is to keep UTC correct to within 0.9 seconds of the mean solar day, and the situation is constantly reviewed by the International Earth Rotation and Reference Systems Service, which issues a six-monthly Bulletin C, declaring or omitting a leap second at the end of each six-month period. Which is why I can’t (at time of writing) say for sure if we’ll have a leap second in 2020.
I’ll add a footnote as soon as I know. Meanwhile, have a Happy New Year.
Footnote: No leap second at the end of 2020, or during 2021.
or

Fascinating. Very clearly described., I wondered about the traditional issue of no leap year if the year was divisible by 4 but not by 16 . Wasn;t 2004 one of those ?
Happy New Year
The Gregorian convention only drops a leap year on centuries not evenly divisible by 400. Like this:
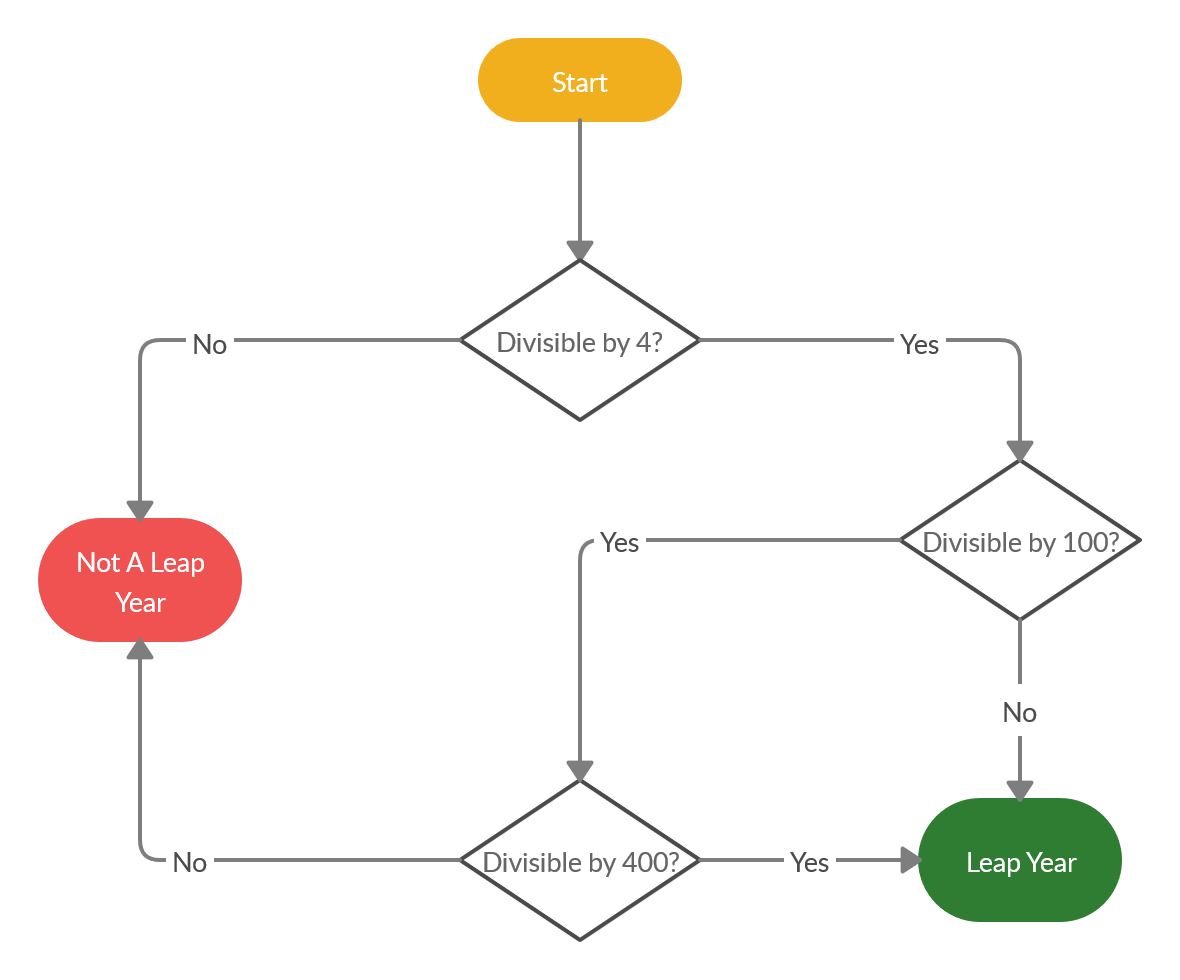
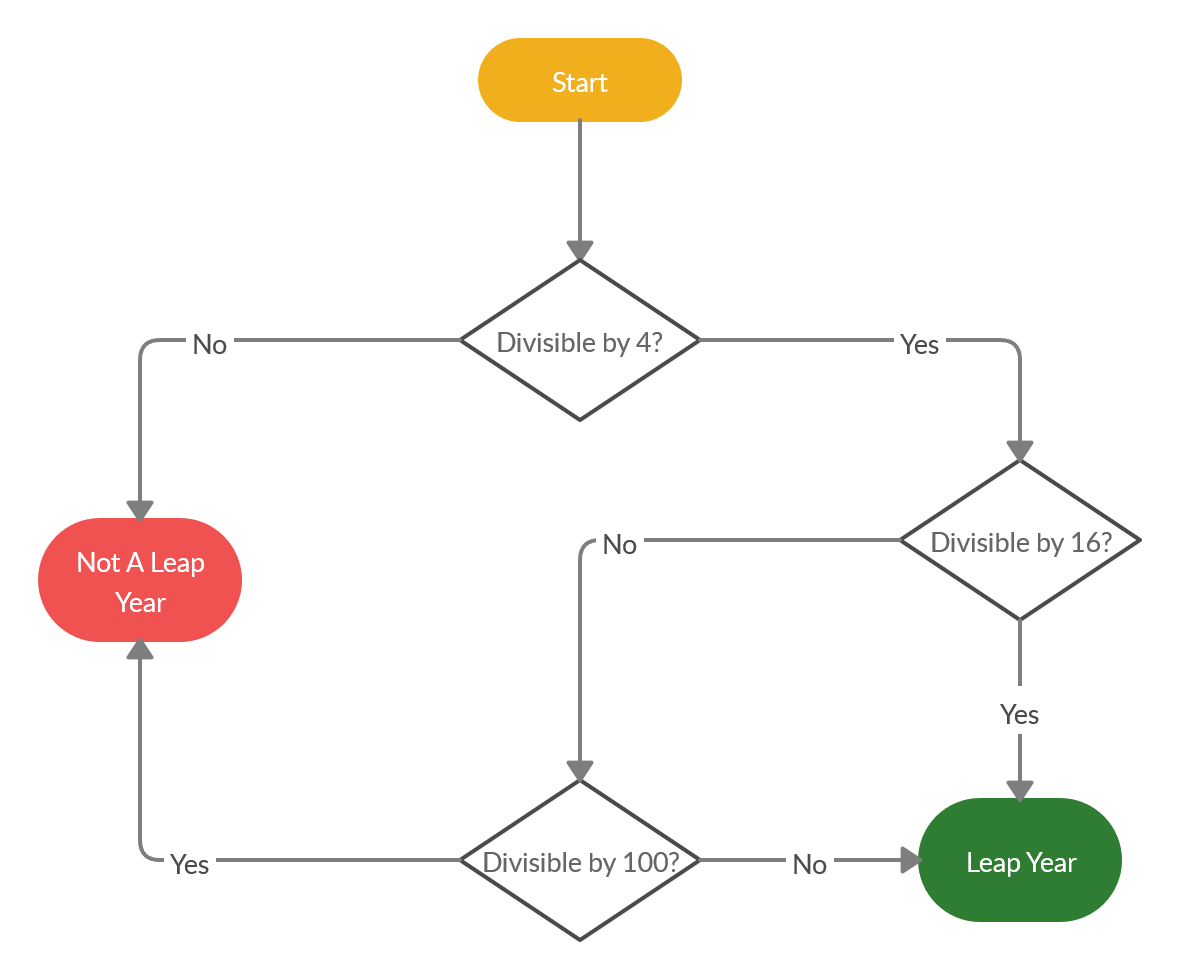
The only time I’ve seen 16 crop up is in a rather counterintuitive algorithm we used to use back in the day when people worried about coding efficiency:
This does a couple of checks that are very quick in binary (even division by 4 and 16), and avoids the more time-consuming check (division by 100) unless it’s needed at the end.
Last year the rotation of the earth’s crust accelerated so that we were rotating faster than we were 200 years ago. That actually reduced the leap second deficit for a brief interval, so a leap second during 2020 is extremely unlikely. See the predictions in IERS Bulletin A that show UT1-UTC will be only -0.29480 at the beginning of next year.
Thanks for that. They do seem to be predicting a much slower change in 2020 than the average rate has been in 2017-2019. Inteesting.
Ironically, the earth started rotating faster right about the inception of leap seconds, and overall has kept doing that for the past 50 years. See the plots for the long history of speedup and slowdown https://www.ucolick.org/~sla/leapsecs/dutc.html